Logarithmic Functions Their Graphs And Applications

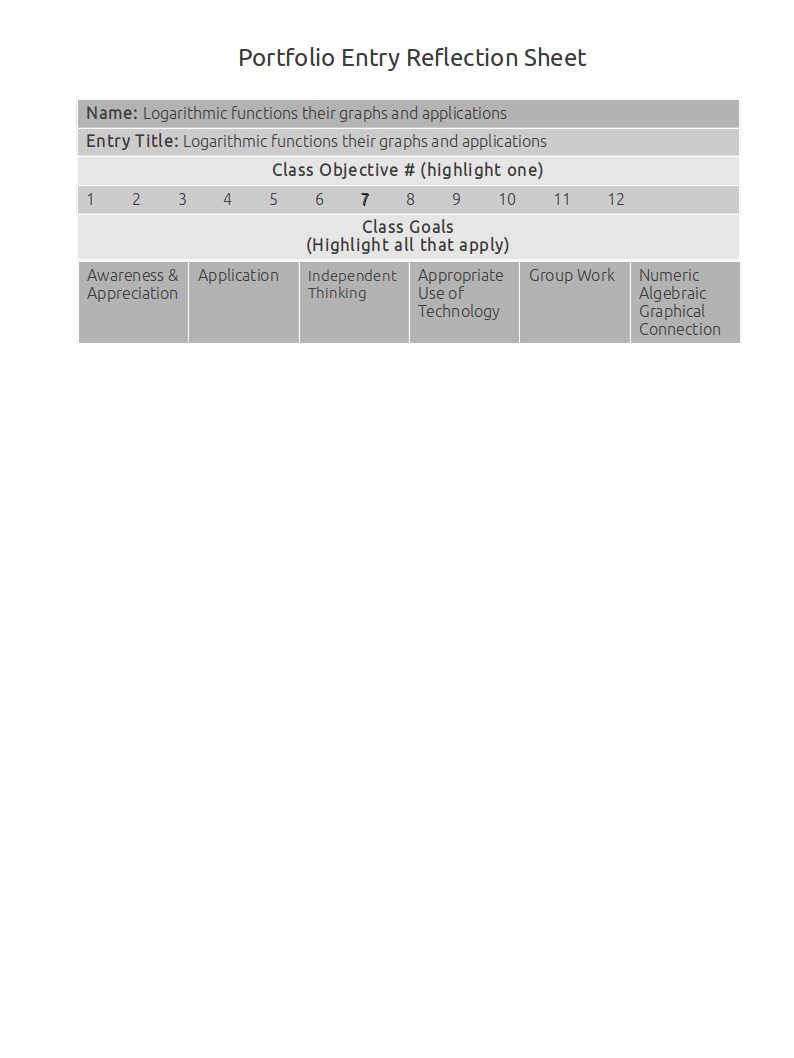
Rewriting exponentials into logarithms and logarithms into exponentials using common log, natural log, and logarithms of other bases

Source: I made these up.

Explanation:

This artifact demonstrates rewriting exponentials into logarithms and logarithms into exponentials using common log, natural log, and logarithms of other bases.

1. Exponential \(\rightarrow\) Common Log
2. Commong log \(\rightarrow\) Exponential
3. Exponential \(\rightarrow\) Natural Log
4. Natural log \(\rightarrow\) exponential

Artifact:

1. \(4^x = 6 \rightarrow log_4 6 = x\)
2. \(log_2 2 = x \rightarrow 2^x = 2\)
3. \(e^x = e \rightarrow ln(e)\)
4. \(ln(8) \rightarrow e^x = 8\)

Properties of logarithms

Source: Notes

Explanation:

This artifact demonstrates properties of logarithms.

1. This problem demonstrates the Product Rule.

\(log_b {rs} = log_b r + log_b s\)

2. This problem demonstrates the Quotient Rule.

\(log_b {r \over s} = log_b r - log_b s\)

3. This problem demonstrates the Power Rule.

\(log_b {r^c} = log_b r * c\)

Artifact:

1. \(log(x+6) + log(x-2) = 2\)

\[log((x+6)(x-2)) = 2\]\[log(x^2 + 4x -12) = 2\]\[10^2 = x^2 + 4x -12\]\[x^2 + 4x -112 = 0\]\[x \approx 8.77 \text{ or } x \approx -12.770\]

2. \(log(x+6) - log(x-2) = 2\)

\[log({(x+6) \over (x-2)}) = 2\]\[10^2 = {(x+6) \over (x-2)}\]\[x \approx {26 \over 9}\]

3. \(\text{Solve for }log_4 117\)

\[4^x = 117\]\[log(4^x) = log(117)\]\[x * log(4) = log(117)\]\[x = {log(117) \over log(4)} = 3.435\]

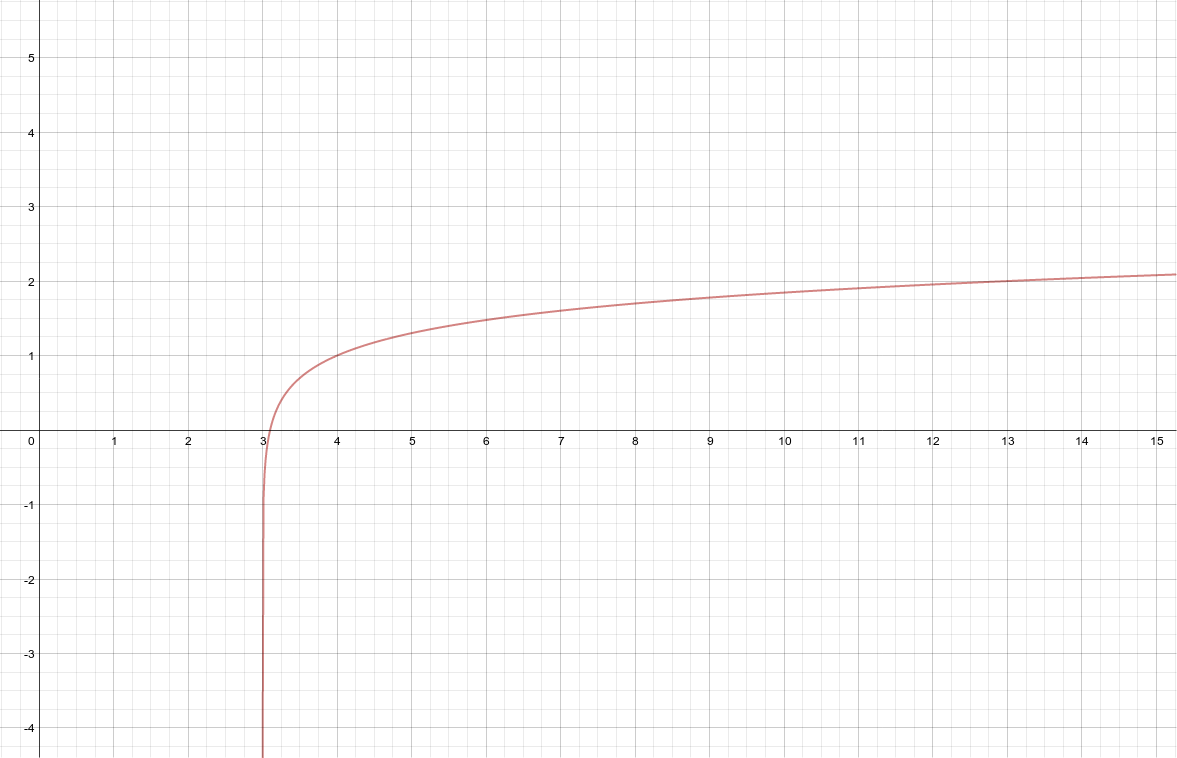
Graphs of logarithms

Source: Made it up.

Explanation:

This artifact demonstrates graphs of logarithms.

I started with the base function \(y = log(x)\) and manipulated it into \(log(x-3)+1\).

The formula \(y = log(x)\) is the same as \(10^y = x\), which is easier to evaluate (for y).

Artifact:

Graph \(log(x-3)+1\)

x	y
0.01	-2
0.1	-1
1	0
10	1

x+3	y+1
3.01	-1
3.1	0
4	1
13	2

Applications of logarithms

Source: #53 from Section 3.4

Explanation:

This artifact demonstrates applications of logarithms.

In the first step I demonstrate that I know how to re-write common logs into exponential form.

After that, I can plug in the given x value (40 ft) and the equation becomes linear and easy to solve.

Awareness and Appreciation:

In this artifact I demonstrate that I am aware that I am error-prone even if the problem is easy, and that I can appreciate double-checking my answers.

Artifact:

The relationship between intensity I of light (in lumens) at a depth of x feet in Lake Superior is given by \(log({I \over 12}) = -0.00235x\)

What is the intensity at a depth of 40 ft?

\[10^{-0.00235x} = {I \over 12}\]\[0.805358 = {I \over 12}\]\[I = 9.664541294 \text{ lumens}\]\[\begin{split}\text{Checking my work...}\\\end{split}\]\[log({9.664541294 \over 12}) = -0.94\]\[-0.00235 * 40 = -0.94\]