Polar Coordinates And Equations¶

How to graph polar coordinates¶

Source:

Explanation:

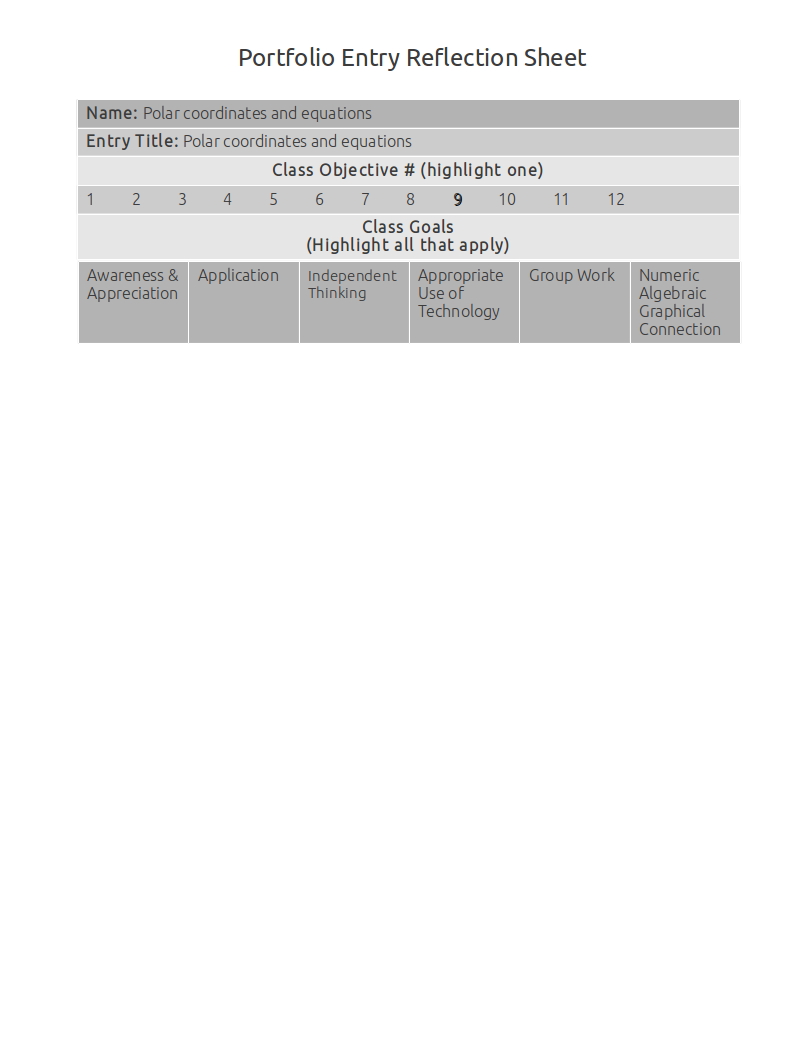
This artifact demonstrates how to graph polar coordinates.

In the polar coordinate \(P(2, { \pi \over 3})\), the directed distance is 2, and the directed angle is \(\pi \over 3\).

So the pole starts at 2 on the O ray, and swivels out by \(\pi \over 3\) degrees.

Artifact:

Plot the point \(P(2, { \pi \over 3})\)

Converting polar coordinates to rectangular coordinates and rectangular to polar¶

Source: Notes, Section 6.4 example 3A

Explanation:

This artifact demonstrates converting polar coordinates to rectangular coordinates and rectangular to polar.

In this example I use the equation \(r^2 = x^2 + y^2\) to solve for the directed distance (x) and \(tan^{-1}({y \over x})\) to solve for the directed angle (y).
In this example I use the formulas \(x = r \cos \theta \text{ and } y = r \sin \theta\), and my knowledge of the unit circle, to calculate the approximate values of x and y.

Artifact:

Convert the rectangular coordinate (2,7) into a polar coordinate.

\(r = \sqrt{2^2 + 7^2} = \sqrt{53}\\ tan^{-1}({7 \over 2}) = 74^\circ\)

Polar coordinate = \((\sqrt{53}, 74^\circ)\)

Convert the polar coordinate \((3, {5\pi \over 6})\) into a rectangular coordinate.

\(x = r \cos \theta\\ x = 3 \cos {5 \pi \over 6}\\ x = 3(-{\sqrt{3} \over 2}) \approx -2.60\)

\(y = r \sin\theta\\ y = 3 \sin {5 \pi \over 6}\\ y = 3({1 \over 2}) \approx 1.5\)

Rectangular coordinate = \((-2.60, 1.5)\)

Converting polar equations to rectangular equations and rectangular to polar¶

Source: Section 6.4 Example 5 and Example 6

Explanation:

This artifact demonstrates converting polar equations to rectangular equations and rectangular to polar.

\(r^2 = x^2 + y^2\\ x = r \cos \theta\\ y = r \sin \theta\)

Here I simplify \(r = 4 \sec \theta\) into \(r \cos \theta\) so I can substitute for \(x\) using the formula \(x = r \cos \theta\). The answer is the line \(x = 4\).
Here I simplify the original equation into x’s and y’s in both the second and first degree because I can subsitute them with the conversion formulas \(\\x = r \cos \theta \text{ and } y = r \sin \theta\) to convert them from rectangular form into polar form.

Artifact:

Convert \(r = 4 \sec \theta\) to rectangular form.

\[r = 4 \sec \theta\]\[{r \over \sec \theta} = 4\]\[r \cos \theta = 4\]\[x = 4\]

Convert \((x-3)^2 + (y-2)^2 = 13\) to polar form.

\[(x-3)^2 + (y-2)^2 = 13\]\[x^2 - 6x + 9 + y^2 -4y + 4 = 13\]\[x^2 + y^2 -6x -4y = 0\]\[r^2 - 6r \cos \theta -4r \sin \theta = 0\]\[r(r - 6 \cos \theta - 4 \sin \theta) = 0\]\[r = 0 \text{ or } r - 6 \cos \theta - 4 \sin \theta = 0\]

Graphs of polar equations¶

Source: Section 6.5 Example 5

Explanation:

This artifact demonstrates graphs of polar equations.

From graphing the polar equation \(r = 3 -3 \sin x\) in radian/function mode, I can tell that the maximum r value is 6 because that is the highest y value you can ever get on this particulur sinusoid.

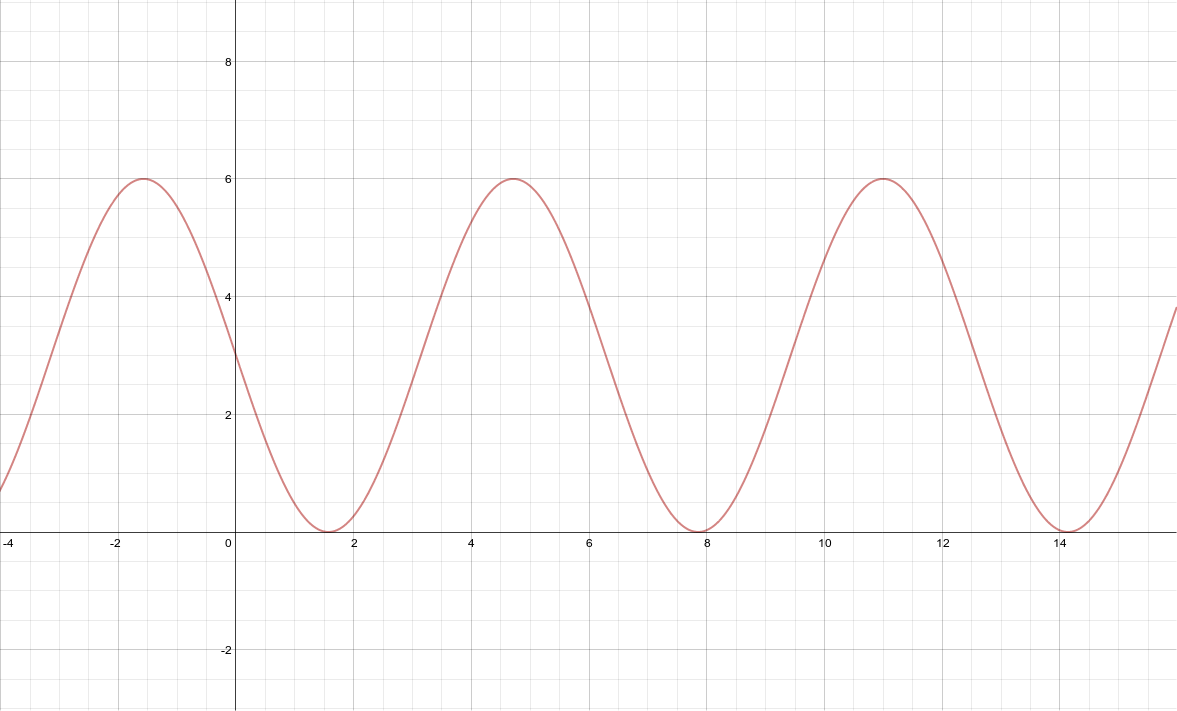
The rest of the information can be gathered visually.

Artifact:

Analyze the graph of \(r = 3 -3 \sin \theta\).

Domain: All real numbers

Range: [0, 6]

Symmetric about the y-axis

Maximum r-value = 6